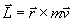lunes, 9 de mayo de 2011
Inercia y Conservación del Momento Angular : Análisis de Diversas Situaciones
Situaciones
La bailarina aprovecha la conservación del momento angular para aumentar o disminuir su rapidez angular.Al extender los brazos aumenta su inercia rotacional,disminuyendo su rapidez y viceversa
En el caso de un equilibrista sucede lo mismo ya que al utilizar una barra más larga aumenta su inercia rotacional, disminuyendo su rapidez y sus probabilidades de caerse
La bailarina aprovecha la conservación del momento angular para aumentar o disminuir su rapidez angular.Al extender los brazos aumenta su inercia rotacional,disminuyendo su rapidez y viceversa
En el caso de un equilibrista sucede lo mismo ya que al utilizar una barra más larga aumenta su inercia rotacional, disminuyendo su rapidez y sus probabilidades de caerse
Relación Torque - Momento angular
Torque
Medida de la capacidad de una fuerza para provocar una rotación .Se mide en [N m] y se define como:
t=r * F * senº
Relación Torque - Momento angular
La fuerza neta que actua sobre un cuerpo es equivalente al cambio del momento lineal en un intervalo de tiempo entonces definimos F como:
(IMAGEN 2.12PAGINA 46)
Si remplazamos F en la formula de torque anterior obtenmos :
IMAGEN 2.13LIBROPAGINA 46
y a partir de la imagen del LIBRO TUERCA definimos el módulo del momento angular como :
IAMGEN 2.14LIBROPAGINA 46
De modo que las ecuaciones 2.13 nos idican que
IMAGEN 2.15
Dándonos como resultado que el cambio o variación del momento angular del sistema mecánico ,sea este un conjunto de partículas o un objeto rígido se debe al torque
Medida de la capacidad de una fuerza para provocar una rotación .Se mide en [N m] y se define como:
t=r * F * senº
Relación Torque - Momento angular
La fuerza neta que actua sobre un cuerpo es equivalente al cambio del momento lineal en un intervalo de tiempo entonces definimos F como:
(IMAGEN 2.12PAGINA 46)
Si remplazamos F en la formula de torque anterior obtenmos :
IMAGEN 2.13LIBROPAGINA 46
y a partir de la imagen del LIBRO TUERCA definimos el módulo del momento angular como :
IAMGEN 2.14LIBROPAGINA 46
De modo que las ecuaciones 2.13 nos idican que
IMAGEN 2.15
Dándonos como resultado que el cambio o variación del momento angular del sistema mecánico ,sea este un conjunto de partículas o un objeto rígido se debe al torque
Momento de Inercia o Inercia Rotacional
Momento de Inercia o Inercia Rotacional
Se considera a la masa del objeto como una medida de su inercia.
Por inercia, al hacer rotar un cuerpo se observa una resistencia al movimiento rotacional, esta resistencia se conoce como inercia rotacional.
Existen dos tipos de sistemas uno que esta compuesto por una sola particula que gira entorno a un eje donde el momento de inercia se define como
Se considera a la masa del objeto como una medida de su inercia.
Por inercia, al hacer rotar un cuerpo se observa una resistencia al movimiento rotacional, esta resistencia se conoce como inercia rotacional.
Existen dos tipos de sistemas uno que esta compuesto por una sola particula que gira entorno a un eje donde el momento de inercia se define como
I=m*r2
Y otro donde el sistema esta compuesto por muchas particulas que giran en torno a un ejeMomento de Inercia o Inercia Rotacional
Momento Angular
Momento Lineal
Propiedad que mantiene el movimiento de un cuerpo hasta que algo lo detiene o cambia su velocidad
P=m*v
Momento Angular
Se define como el producto vectorial del vector posición por el vector momento lineal medido en Kgrm2/s
El modulo del momento angular se relaciona con el modulo de su movimiento lineal y del radio de su curvatura, por lo tanto
L=r x p (p=m*v)
Por lo tanto L=r x m x v
Se puede escribir en terminos de la rapidez angular
L= m x r2 x w
El momento angular posee la misma dirección que la velocidad angular y también se puede determinar su dirección usando la regla de la mano derecha
Propiedad que mantiene el movimiento de un cuerpo hasta que algo lo detiene o cambia su velocidad
P=m*v
Momento Angular
Se define como el producto vectorial del vector posición por el vector momento lineal medido en Kgrm2/s
El modulo del momento angular se relaciona con el modulo de su movimiento lineal y del radio de su curvatura, por lo tanto
L=r x p (p=m*v)
Por lo tanto L=r x m x v
Se puede escribir en terminos de la rapidez angular
L= m x r2 x w
El momento angular posee la misma dirección que la velocidad angular y también se puede determinar su dirección usando la regla de la mano derecha
Suscribirse a:
Entradas (Atom)